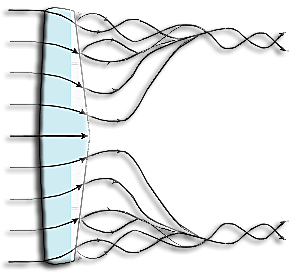
Nappe tourbillonnaire et pertes en bout d'aile schématisées dans le logiciel Heliciel :

 

Aile rectangulaire de longueur 2 mètres Allongement= 4 Finesse (Portance/Traînée) =16	Aile rectangulaire de longueur 9 mètres Allongement= 18 Finesse (Portance/Traînées) =32
Aile pointue de longueur 2 mètres. Allongement= 5 Finesse (Portance/Traînée) =19.	Aile pointue de longueur 9 mètres. Allongement= 33 Finesse (Portance/Traînée) =36

Nous avons vu dans la page traitant des généralités sur les ailes et hydrofoils, que les traînées et portances calculées avec les cx et cz 2D sont des valeurs théoriques, ne prenant pas en compte les phénomènes tourbillonnaires. Ces phénomènes tourbillonnaires sont engendrés par la différence de pression entre l'extrados et l'intrados de l'aile:

C'est la différence de pression entre l'intrados et l'extrados qui génère la portance. On peut donc en déduire que l' intensité des tourbillons Γ(gamma) évoluera en fonction de la portance.

Ces tourbillons modifient la trajectoire du fluide autour de l'aile et induisent des composantes de vitesses dirigées vers le bas. Les Vitesses induites par les tourbillons varient suivant la distance et l' intensité des tourbillons.

Le calcul des vitesses induites par les tourbillons, permet de redéfinir l'angle d'attaque effectif des différentes zones (éléments) de l'aile. L'angle d'attaque effectif permet finalement d' utiliser les performances 2D pour calculer les forces de portance (dL) et de traînée (dD) prenant en compte les phénomènes tourbillonnaires. Ces vitesses induites par les tourbillons varient suivant la portance et la distance du bout de l'aile. On calculera donc ce phénomène pour chaque élément de notre aile ou pale.

Variation de l'angle effectif généré par la Vitesse induite au niveau du profil d' un élément.

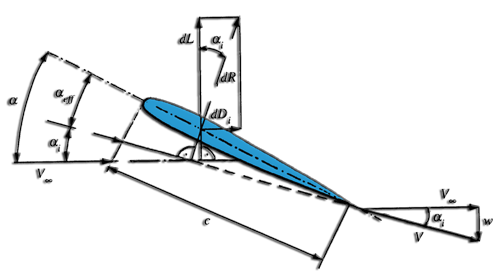
• La vitesse V infinie est la vitesse en amont prise a une distance considérée comme infinie, donc non perturbée par l'aile.
• La vitesse w est la vitesse induite par les tourbillons. La vitesse induite est dirigée vers le bas, elle est donc négative.
• L'angle de a est l'angle d'incidence géométrique.
• L'angle de ai est l'angle d'incidence induite.
• L'angle de aeff est l'angle d'incidence effectif réellement perçu par le profil.

Comment calculer les vitesses induites et l'angle effectif déterminant les performances réelles de notre aile?

Théorie de la ligne portante de Prandtl: Ludwig Prandtl à développé la première méthode permettant l' analyse d'une aile d' envergure finie en 1918 en assimilant tous les filaments tourbillonnaires attachés a une aile a un seul filament nommé "Ligne portante". Les lois et théorèmes définissant les tourbillons permettent un calcul des vitesses induites:

 

• La loi de Kutta-Joukovsky nous donne la relation entre la force de portance(Newtons) et l' intensité du tourbillon attaché (Γ) sur un élément d'aile de longueur L(m) plongée dans un courant de fluide de vitesse V (m/sec) et de masse volumique r(kg/m3):
  • Portance = Γ. r . V. L
  • Γ= Portance / (r . V. L)

pour rappel, La formule de la portance:

Portance(2D)(en Newtons)= Cz . surface élément . r . V²/2

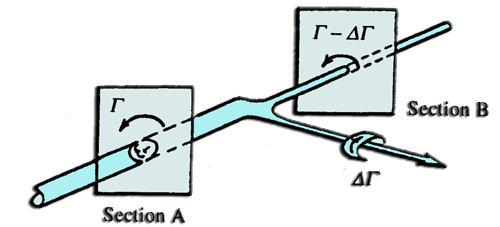
• D'apres le théorème de Helmotz un tourbillon doit être fermé et ne peut finir dans le fluide, ceci implique que la portance d'un élément engendre un tourbillon d' intensité constante (Γ) repartit le long d'une ligne qui doit former une boucle fermée.

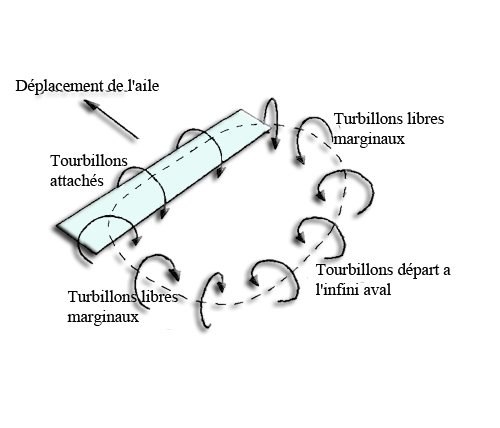
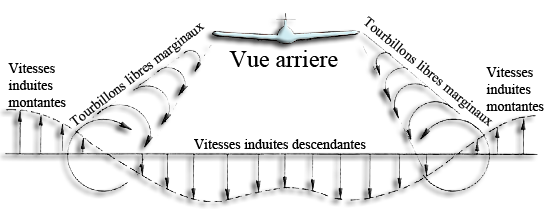
Dans la réalité, lorsque l'aile est en vol, le "tourbillon départ a l' infini aval" est suffisamment éloigné de l'aile pour négliger les vitesses induites qu'il provoque sur l'aile car la vitesse induite par un tourbillons varie comme l' inverse de la distance a l'axe du tourbillon. On ne considère donc que les tourbillons libres marginaux et leurs vitesses induites descendante perçue par l'aile. Les tourbillons libres marginaux sont définis comme semi infini car il commencent au bout de l' élément et se prolongent à l' infini aval.

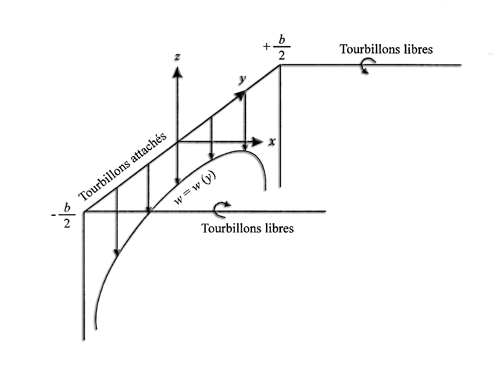
• En remplaçant la force de portance par une ligne de tourbillons attachés au niveau du centre de portance des profils (environ a 1/4 de la corde) qui se prolongent par 2 tourbillons marginaux d' intensité (Γ) constante ,et en négligeant le tourbillon départ, on obtient un système tourbillonnaire en fer a cheval:

 

Système de tourbillon en fer a cheval, d' intensité constante (Γ) équivalente a la portance générant des vitesses induites descendantes.

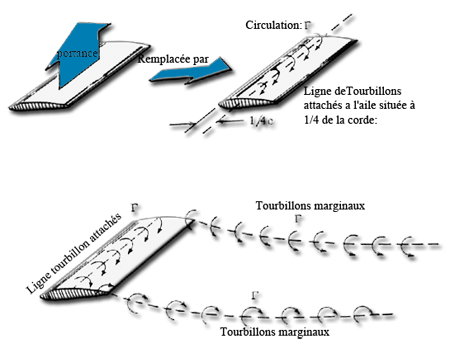
• La loi de biot-Savart nous donne la vitesse induite w(m/sec) en un point (P) situé a une distance h d'un tourbillon marginal d' intensité (Γ) semi infini car il commence au bout de l' élément et se prolonge a l' infini aval. La portance de l' élément (connue grâce au Cz du profil) nous donnant l' intensité , Il nous est donc possible de déterminer la vitesse induite -w au point P:

   

  

  Au point P, la vitesse induite est: w= - Γ/(4ph) .w est négatif car orientée vers le bas.
• Expression des vitesses induites pour un seul système tourbillonnaire isolé:

Posons le point P dans le système des 2 tourbillons en fer a cheval ou la vitesse induite est produite par les 2 tourbillons libres. Le point A est situé en -b/2 et +b/2 et le point P sur l'axe y. La vitesse induite en fonction de la position en y est composée de 2 termes:

1. Le terme -Γ/[4p(b/2+y)] représentant la contribution du tourbillons situé au point A avec y=-b/2
2. Le terme -Γ/[4p(b/2-y)] représentant la contribution du tourbillons situé A avec y=b/2

Qui donnent l' expression de la vitesse induite en fonction de la position y pour un système tourbillonnaire isolé.:

• w(y) = -Γ/[4p(b/2+y)] -Γ/[4p(b/2+y)]
• équivalent à :w(y) = -Γ/(4p) .{b/[(b/2)²-y²]}

Dans cette dernière expression des vitesses induites pour un seul système tourbillonnaire isolé, lorsque la position de y s' approche d' une extrémité (y=b/2 ou y=-b/2), la vitesse induite tend vers moins l' infini. Ce qui ne peut pas correspondre à un représentation réaliste de l'aile d' envergure finie. pour remédier a cela Prandtl amène le concept de ligne portante:

• Expression des vitesses induites pour un ensemble de systèmes tourbillonnaires :La ligne portante

Le premier théorème de Helmotz définissant les lois du mouvement tourbillonnaire stipule que l' intensité Γd'un tourbillon isolé est constante et équivalente a la portance. Une variation de la portance (donc de l' intensité Γ) ne peut pas être représentée par un système de tourbillon isolé. Variation de la portance, donc de l' intensité tourbillonnaire sur une aile:

Le premier théorème de Helmotz indique que la variation de portance sur une aile (donc d' intensité tourbillonnaire) ne peut se faire que si des filaments tourbillonnaires d' intensité égale à la variation d' intensité s' ajoutent ou quittent l'aile:

Un système de tourbillons superposés permet de représente la variation d' 'intensité tourbillonnaire associée à la portance d'une aile. En chaque point de l'aile ou se produit une variation de portance, un tourbillon d' intensité égale à la variation de portance se forme.

Dans la réalité cette nappe de tourbillons se formant sur les bords de fuite se combine ,

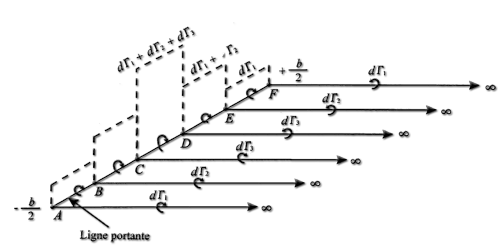
pour former les deux tourbillons marginaux parfois visibles: Mais la variation de portance et d' intensité étant continue et progressive sur l'aile, le nombre de tourbillons en fer a cheval , d' intensité dΓsuperposés sur la ligne portante décrivant la variation d' intensité est infini.

• l' Intensité élémentaire dΓdu tourbillon en fer a cheval correspondant au segment de ligne portante [dy] positionné a y sur la figure ci dessus est donnée par : dΓ= (deltaΓ/delta y).dy
• le tourbillon libre d' intensité dΓva induire une vitesse dw au point y0:

  en utilisant la loi de biot savart définissant la vitesse induite par un tourbillon semi infini:

 

ou l'on remplace :

• Γpar (deltaΓ/delta y).dy, et h par y0-y

on obtient la vitesse induite élémentaire au point y0 produite par le tourbillon libre d' intensité dΓpassant par y :

• dw= - {(deltaΓ/delta y).dy}/{4p.(y0-y)}

La vitesse totale induite en y0 par l'integralité de la couche tourbillonnaire libre de -b/2 à b/2 correspond à:

• w(y0) = -1/(4p) ∫(- +b/2) {(deltaΓ/delta y)/(y0-y)}.dy

L'angle d'incidence induite ai est donc : αi(y0)=atan[-w(y0) / V∞]

 

( références:"Aérodynamique subsonique" de mr Ion Parashivoiu aux éditions de l' école polytechnique de Montréal).

Vous trouverez aussi une description de la théorie de la ligne portante de Prandtl sur le site de mr : j.haertig

http://j.haertig.free.fr/aerodyn_theorique/index.html et notamment ce document pdf :Théorie de la ligne portante de Prandtl